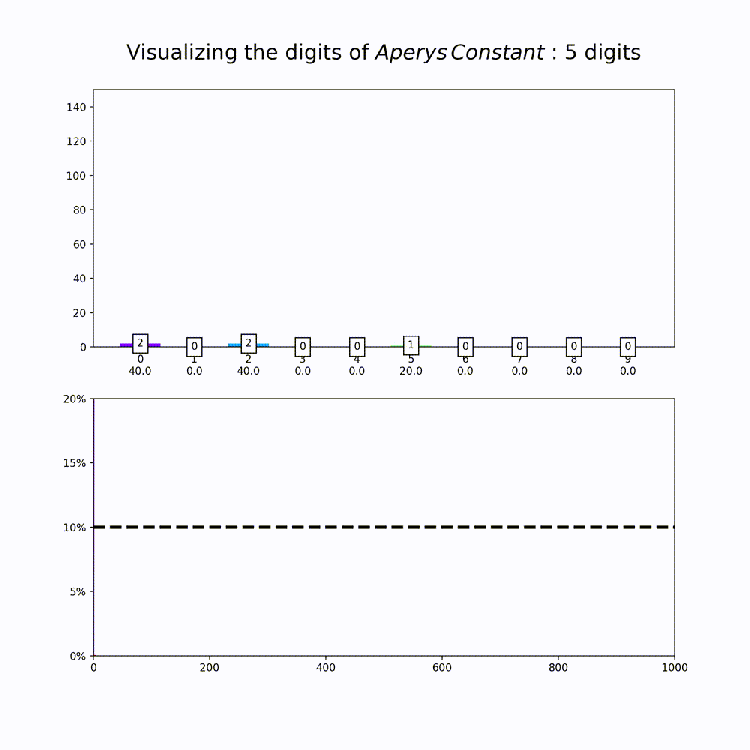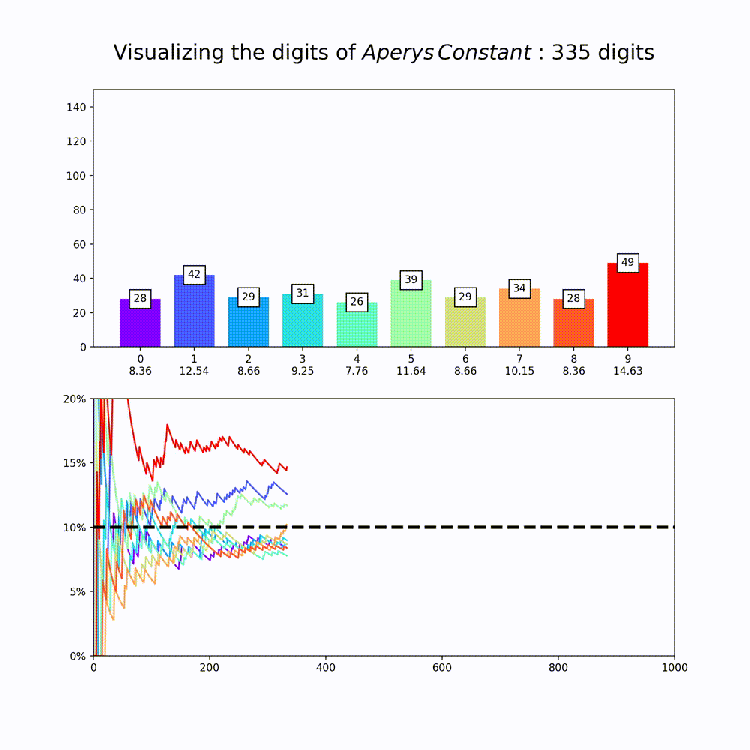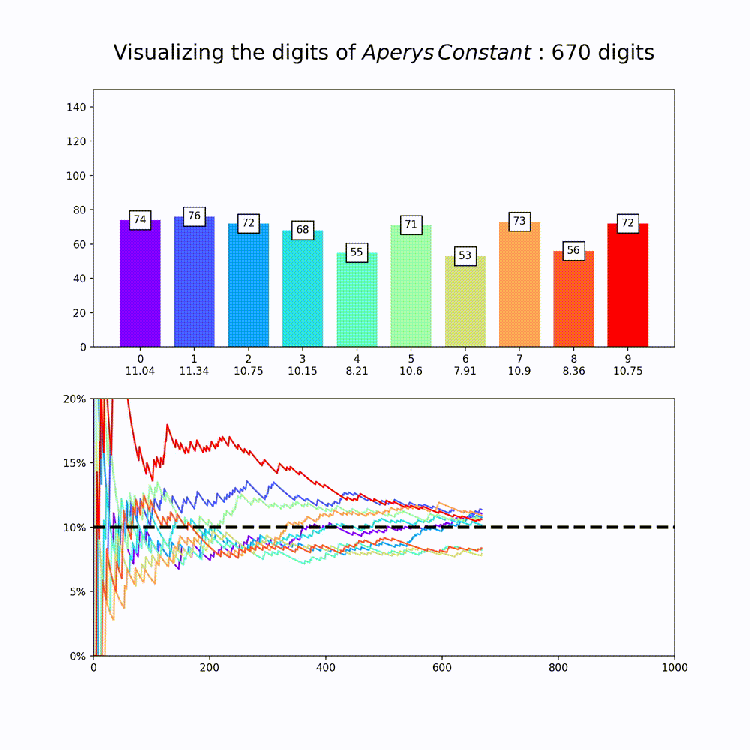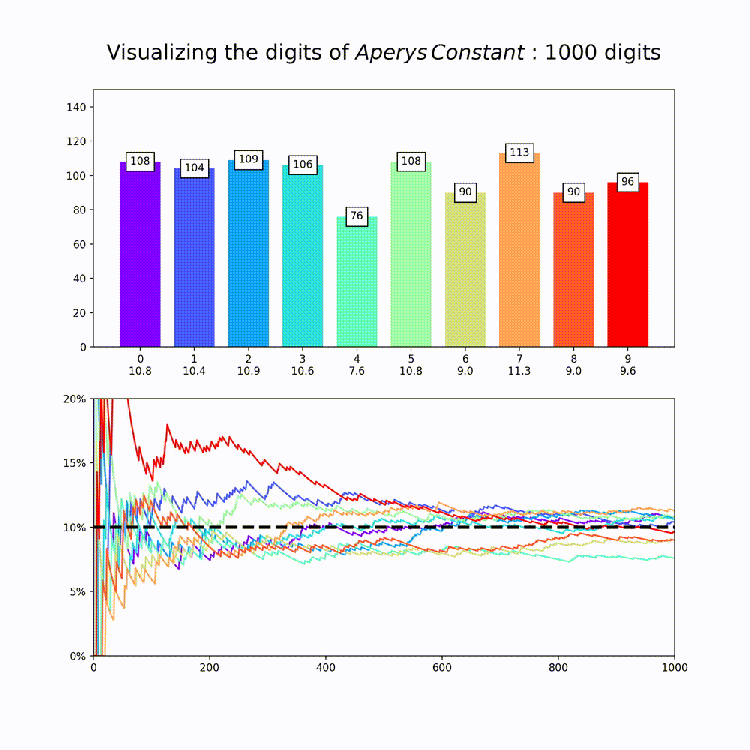
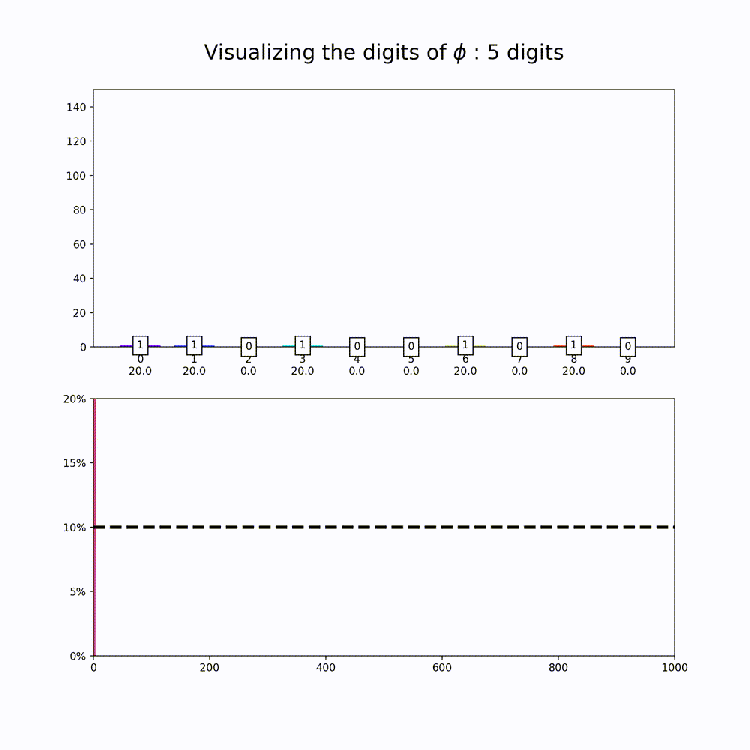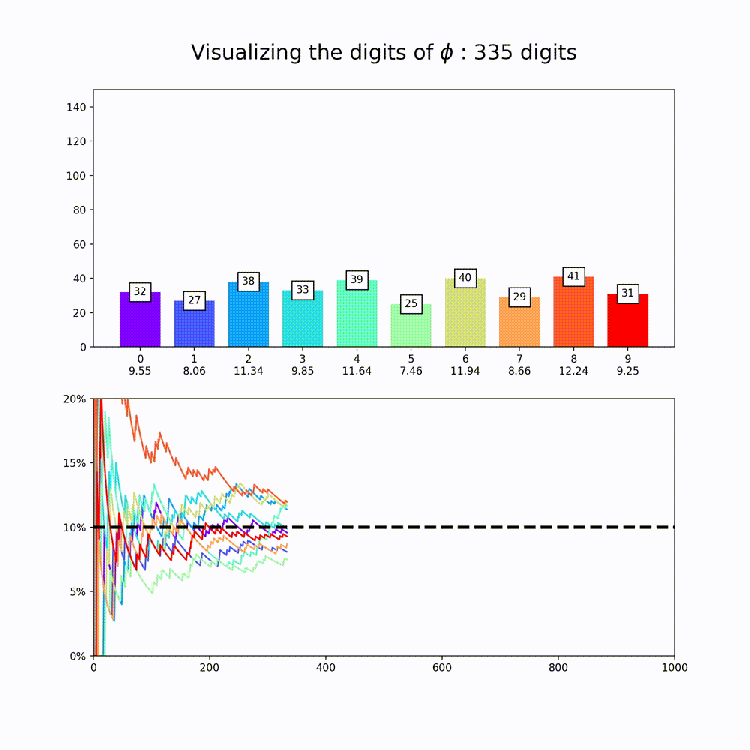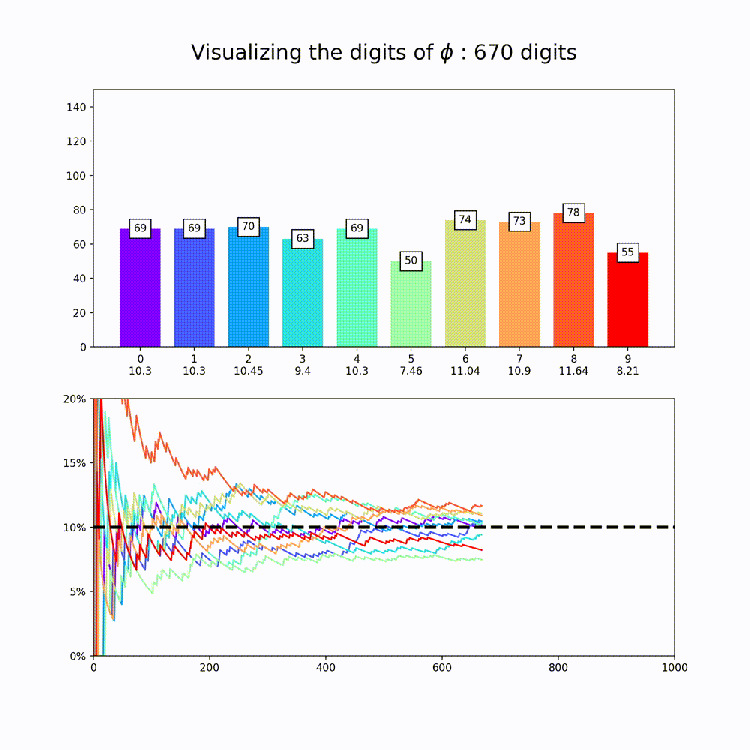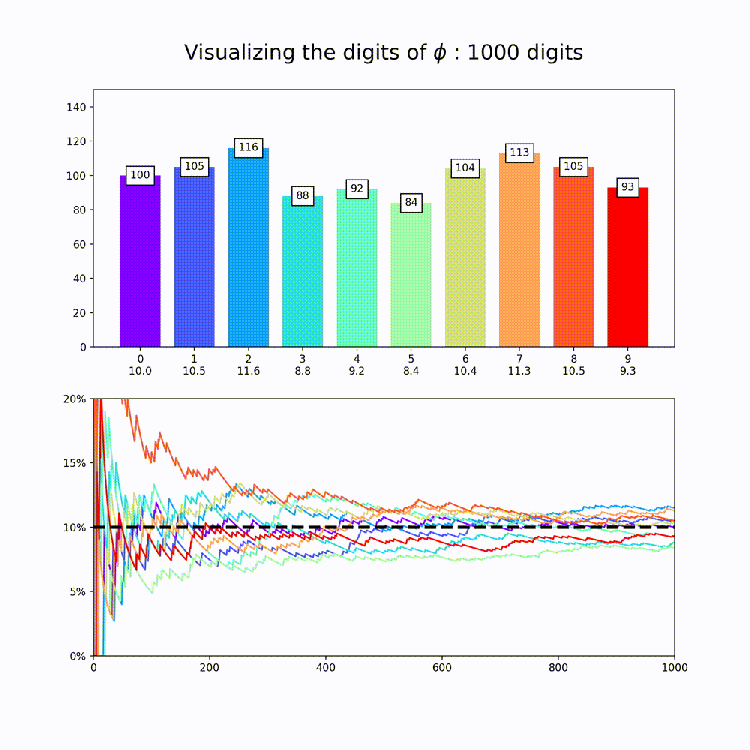
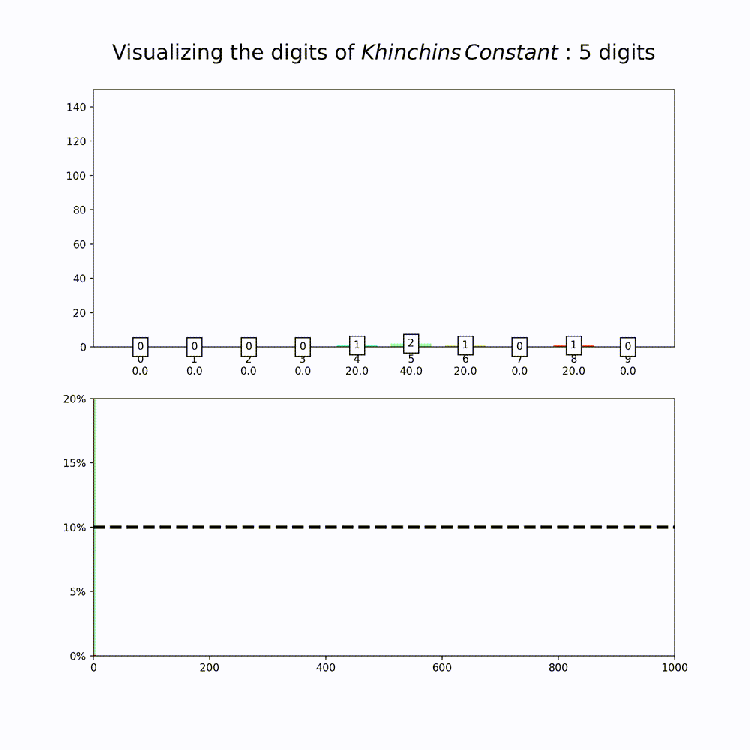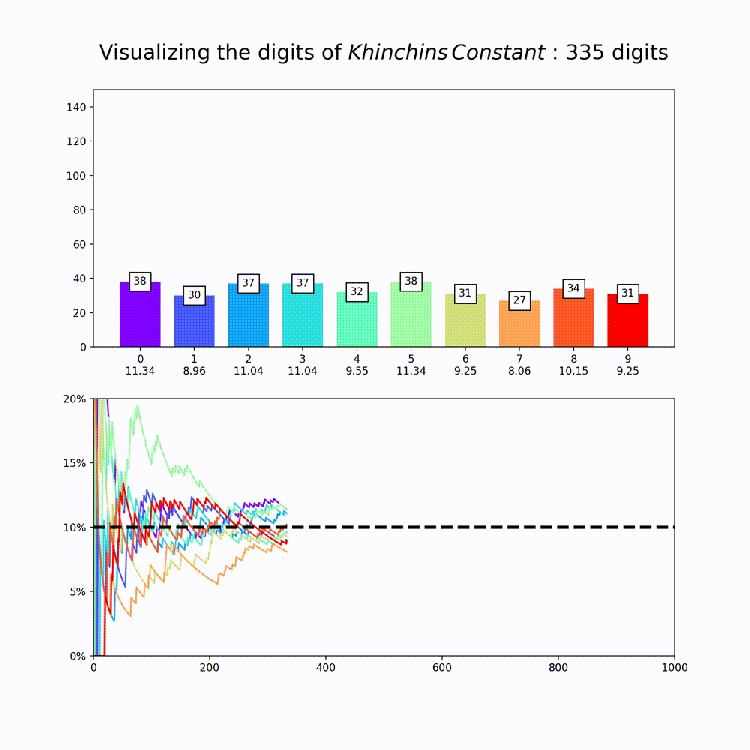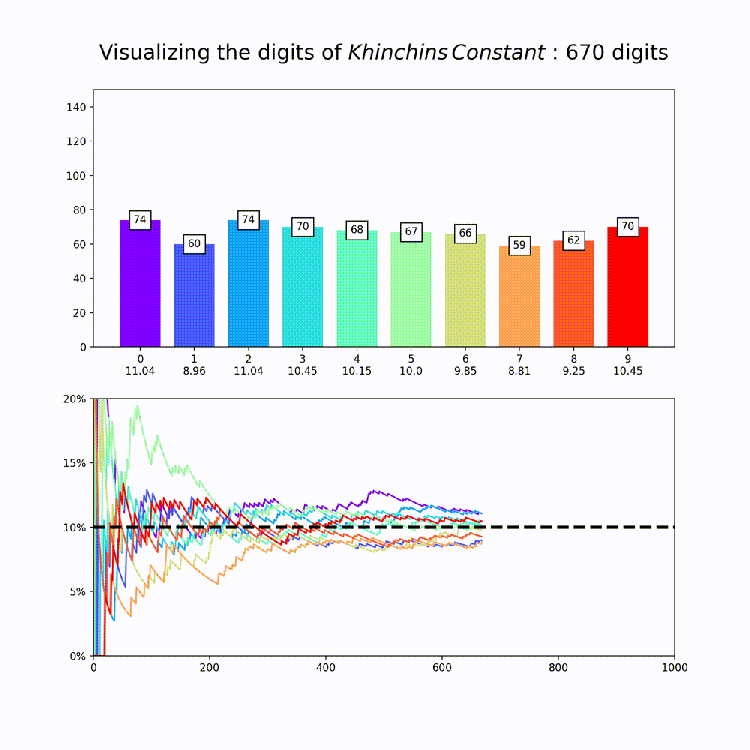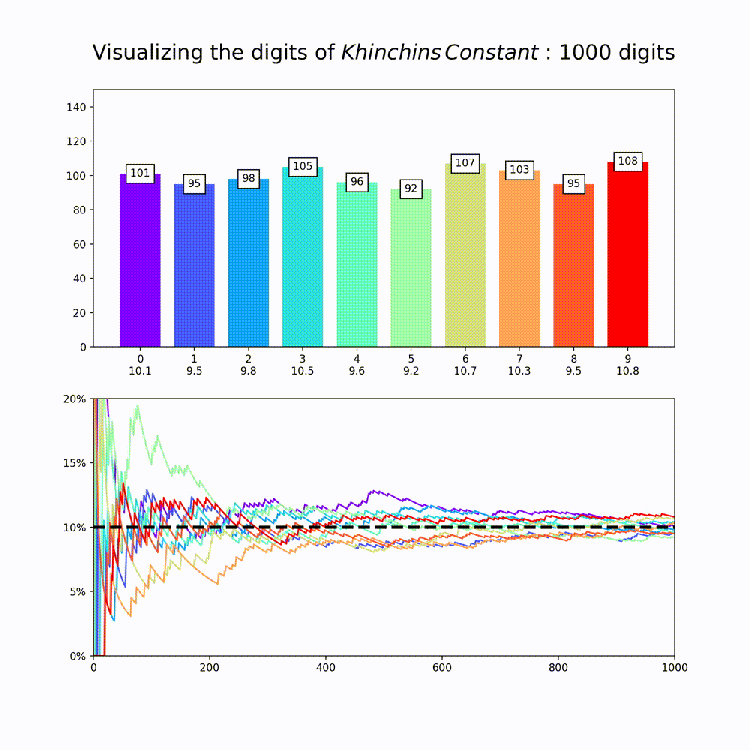
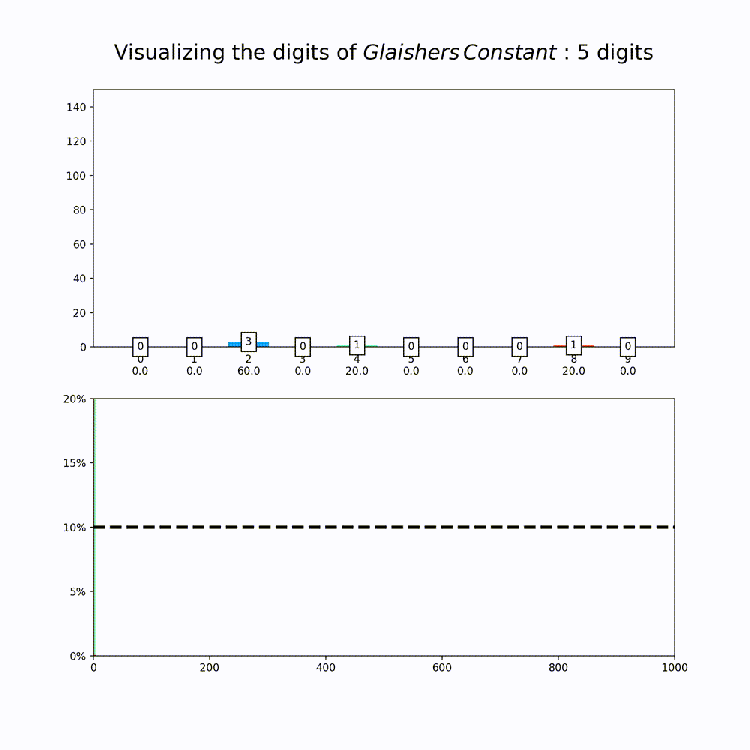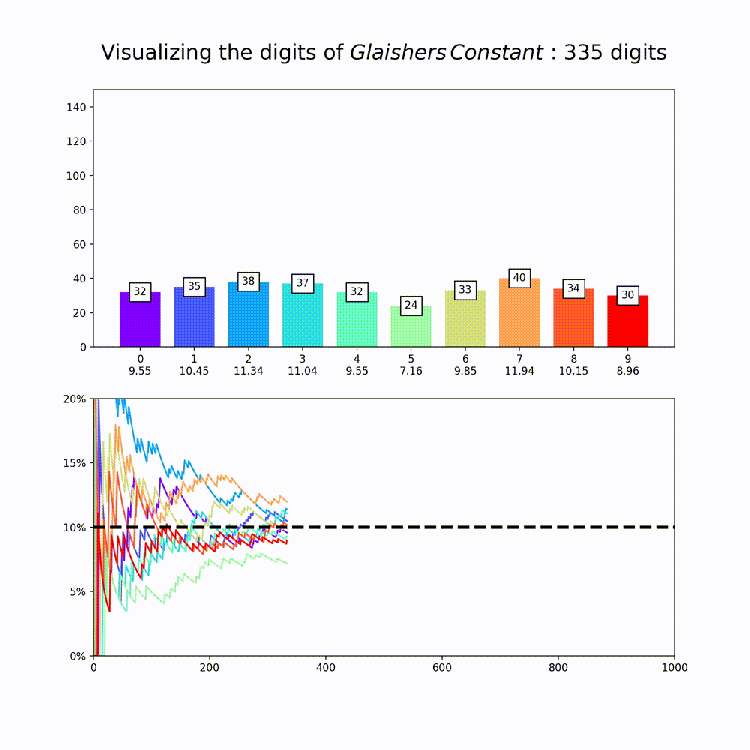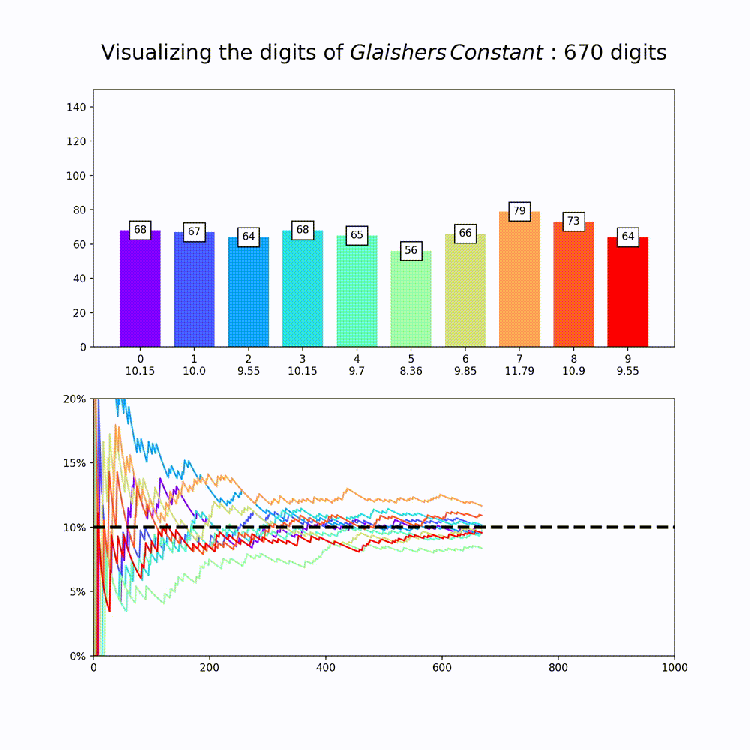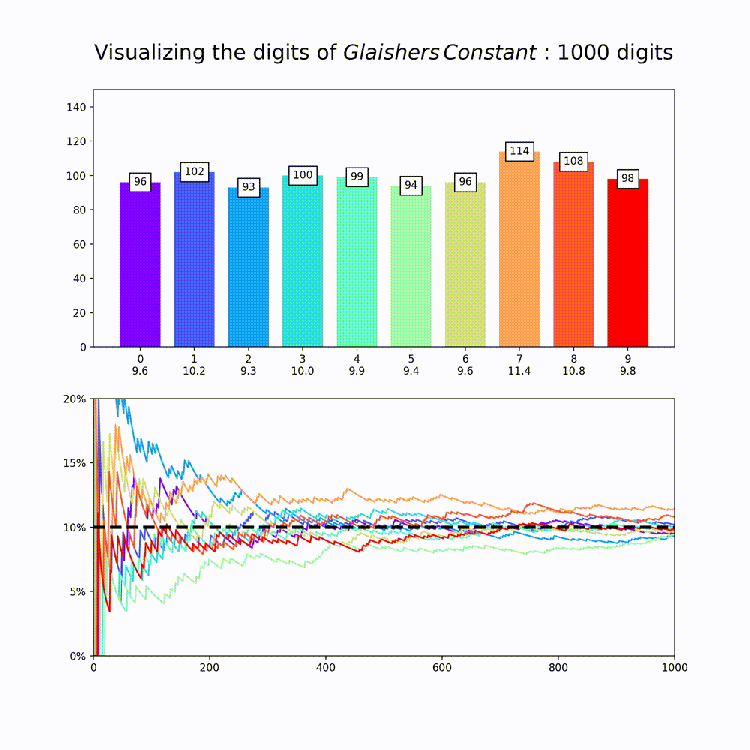
Irrational Number Normality
I was browsing the inter-webs a while back when I stumbled upon this nice visualization of the digits of Euler’s number. Original Linked Here: [https://www.reddit.com/r/dataisbeautiful/comments/b4azz7/visualizing_first_1000_digits_of_eulers_number_oc/]
I was curious how other numbers would look presented in the same way, and I figured I could reproduce the plot pretty well with python and matplotlib.
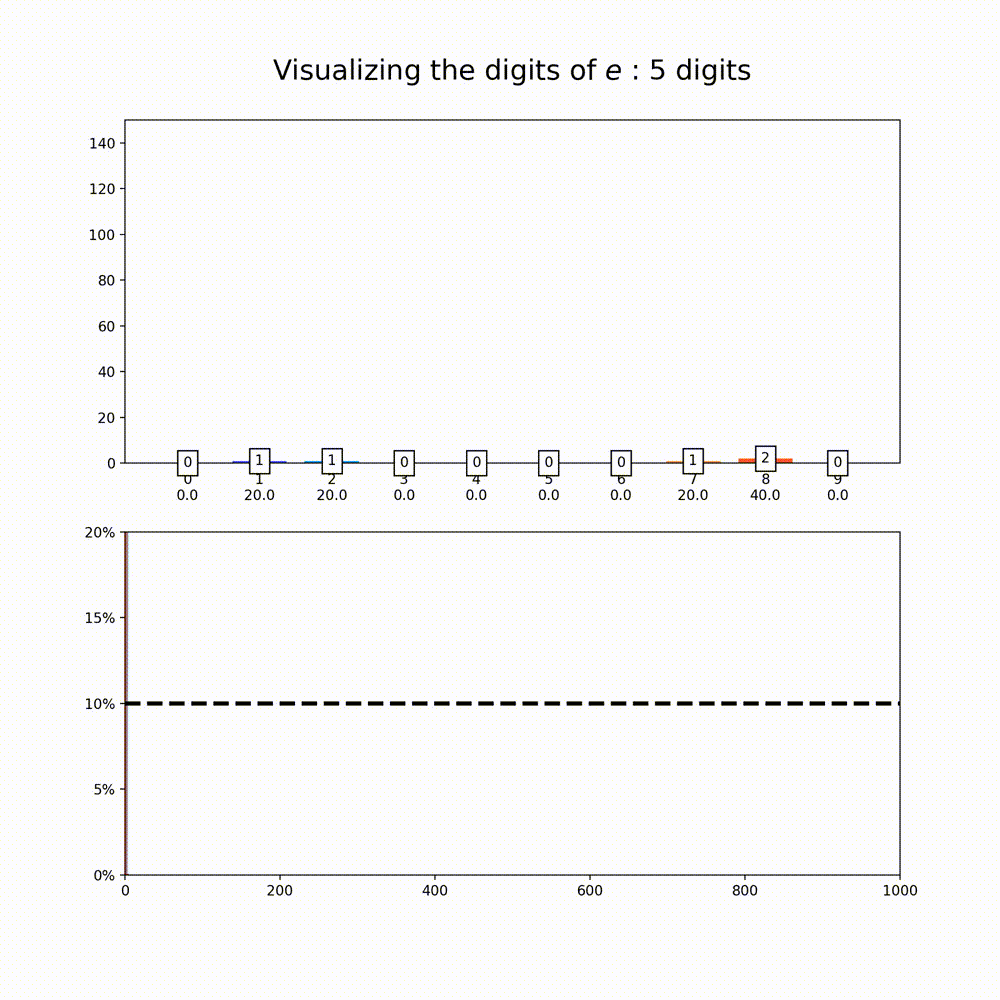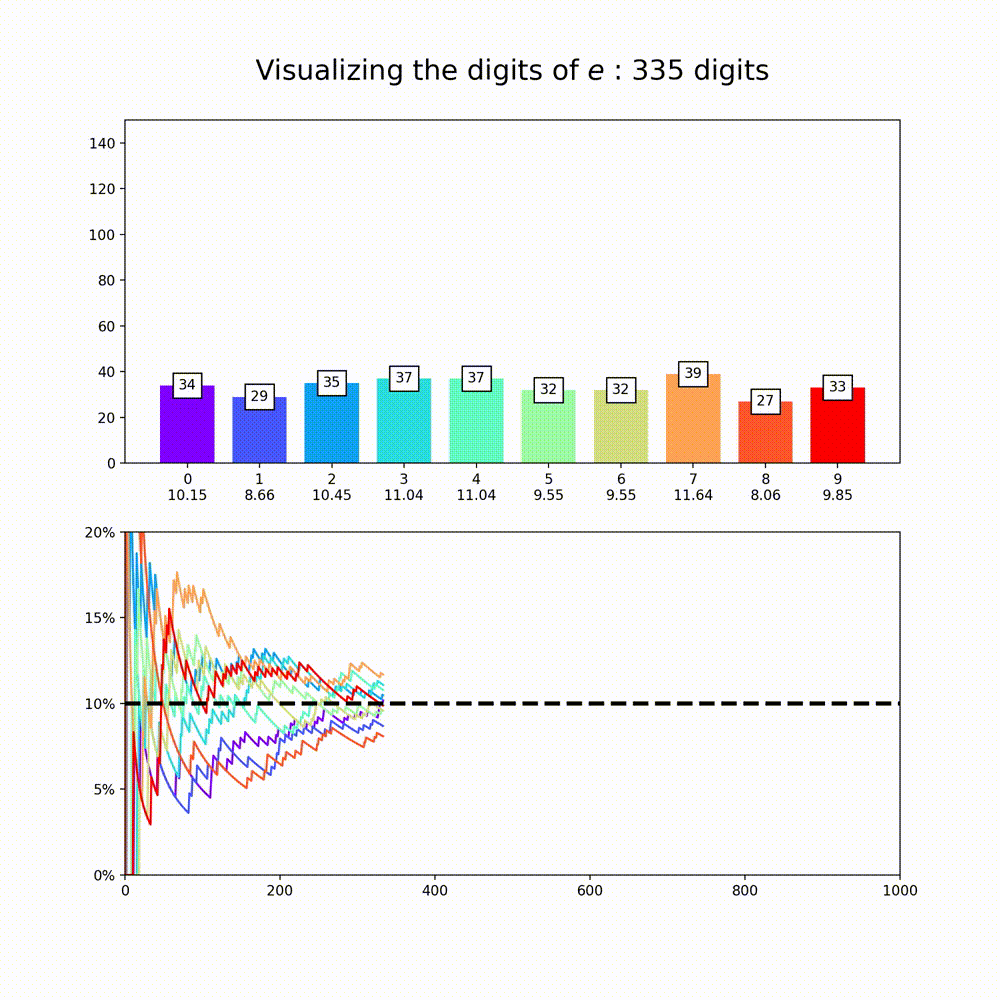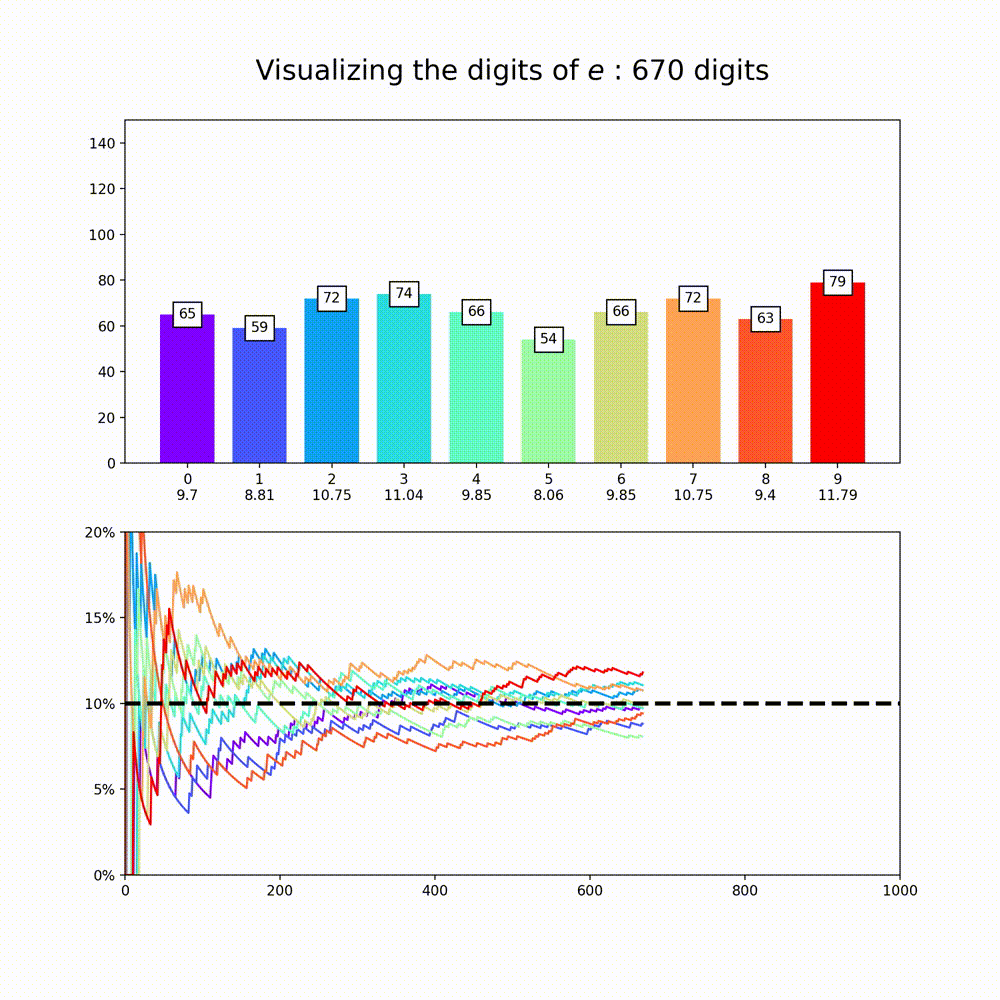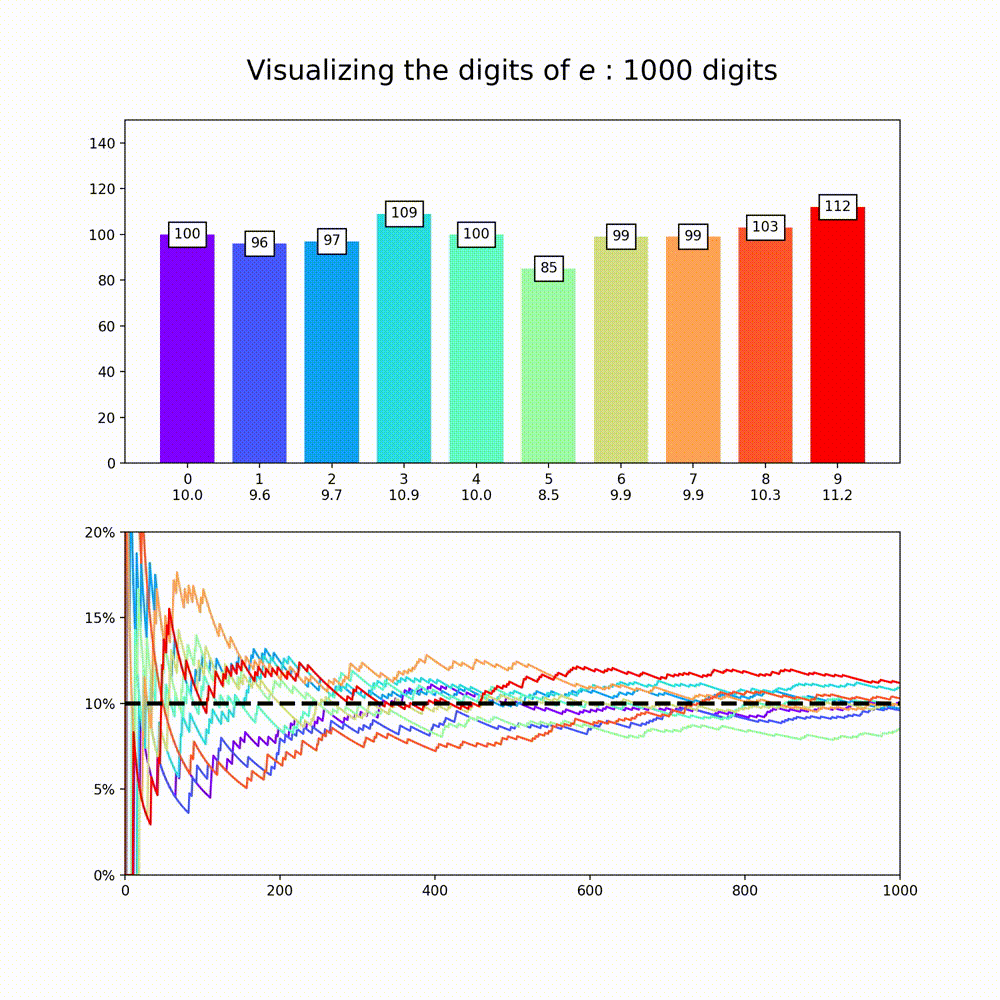
This plot is a nice way to illustrate the property of “normality”, which means that a numbers digits are uniformly distributed in every base. So for base 10, all digits should appear about 10% of the time. The animation above amounts to a test of the normality of e in base 10.
Now for the code, I start out importing a few modules that will be useful. I find numpy, matplotlib and mpmath (a module that specializes in arbitrary precision calculations) are sufficient.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
import matplotlib.ticker as ticker
from mpmath import *
Next we define two convenience functions. The first calculates out our constant to a given precision and splits off only the decimal digits. We take advantage of mpmath here and use their pre-defined constants, in this case 
def makenum(digits):
mp.dps=digits
num = str(1*pi).split('.')[1]
return num
def cumnums(innum):
cumdata=[]
for i in range(1,len(innum)):
num= innum[0:i]
data = [num.count('0'),num.count('1'),num.count('2'),num.count('3'),num.count('4'),num.count('5'),num.count('6'),num.count('7'),num.count('8'),num.count('9')]
cumdata.append(100*np.asarray(data)/i)
return np.asarray(cumdata).T
Lastly we have the main part of the code. This code sets up the labels, the scale as a function of the maximum number of digits, and sets the axis labels and title. It saves all of this to a folder in the current directory called ‘output’,
def makeplot(digits,number,name):
maxdigits = 1000
#samples a subset of numbers
num = number[:digits]
#counts how many digits in each
data = [num.count('0'),num.count('1'),num.count('2'),num.count('3'),num.count('4'),num.count('5'),num.count('6'),num.count('7'),num.count('8'),num.count('9')]
#sets up labels for bars
label = ['0','1','2','3','4','5','6','7','8','9']
#calculates percentages
perc = np.round((100*np.asarray(data)/digits),2)
#combines label and percentages together
labels=[]
for i in range(len(label)):
labels.append(label[i] +'\n'+str(perc[i]))
x=np.arange(len(labels))
#defines colormap
cs = cm.rainbow(x/np.max(x))
cumdata = cumnums(num)
alldata=[cumdata[0],cumdata[1],cumdata[2],cumdata[3],cumdata[4],cumdata[5],cumdata[6],cumdata[7],cumdata[8],cumdata[9]]
#from matplotlib documentation
#https://matplotlib.org/3.1.1/gallery/lines_bars_and_markers/barchart.html
def autolabel(rects):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
ax[0].annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, -5), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom',bbox=dict(facecolor='white'))
#creates plot
fig,ax = plt.subplots(nrows=2,figsize=(10,10))
bars = ax[0].bar(labels,data,color=cs,width=0.75,align='center')
autolabel(bars)
ax[0].set_ylim(0,0.15*maxdigits)
for i in range(len(alldata)):
ax[1].plot(alldata[i],color=cs[i],zorder=1)
ax[1].set_ylim(0,20)
ax[1].set_xlim(0,maxdigits)
ax[1].hlines(10,0,maxdigits,linestyle='--',color='k',lw=3,zorder=2)
ax[1].yaxis.set_major_locator(ticker.MultipleLocator(5))
plt.yticks([0,5,10,15,20], ['0%','5%','10%','15%','20%'])
ax[0].set_title(r"Visualizing the digits of $\pi$ : "+str(digits)+" digits \n", fontsize=20)
plt.savefig('./output/'+str(name)+'.png',dpi=200)
plt.close()
Lastly, all that’s left is to loop over this function to generate the images:
digrid=np.arange(5,1005,5)
number = makenum(1005)
for i in range(len(digrid)):
print(digrid[i])
makeplot(digrid[i],number,i)
It should also be noted that this script is not particularly efficient, calculating the cumulative data within the loop is wasteful since one could simply calculate it once and pass it into the function which could then truncate it. Since we’re making plots with only a few digits (~1000) this won’t matter too much. However calculating our constant to 1000 digits is very time consuming. Its for this reason we calculate the number outside of the loop and then pass it into the function, rather than doing so independently for each image.
Regardless of your feelings about the code efficiency, the above code will output a sequence of images that can then be converted into a .gif animation. I like to use ffmpeg for these things, and I have had the best results by converting through an .avi first. I use the following two commands.
#To be executed in the output folder, produces file NAME.avi #in the above directory.
ffmpeg -framerate 15 -i %d.png -qscale:v 0 ../NAME.avi
#executed in the above directory, produces the .gif
ffmpeg -i $NAME.avi -vf scale=1000:1000 $NAME.gif
More conveniently, I package all the files into a bash script which takes the filename as an input. It makes the graphic then removes all the original .png files from the output
echo $1
cd output
ffmpeg -framerate 15 -i %d.png -qscale:v 0 ../$1.avi
cd ..
ffmpeg -i $1.avi -vf scale=1000:1000 $1.gif
rm $1.avi
cd output
rm *.png
Now that we have our code together, I produced similar graphs for the other constants in mpmath [Documentation Here: http://mpmath.org/doc/current/functions/constants.html%5D. This could of course be expanded to any constant you want – just set the number variable that’s being passed to makeplot whatever you want. All together, here are the constants:
Finally, its worth saying that while this is good evidence for the normality of each of these constants in base 10, its extremely hard to prove normality for any given number and so for most (maybe even all) of these numbers it’s actually unknown if they are truly normal or if they just appear to be so for small numbers of digits.
Github Link to Code: https://github.com/r-zachary-murray/Irrational_Normality
degenerate-states.com 