A Simple Orbital Resonance

A Simple Orbital Resonance

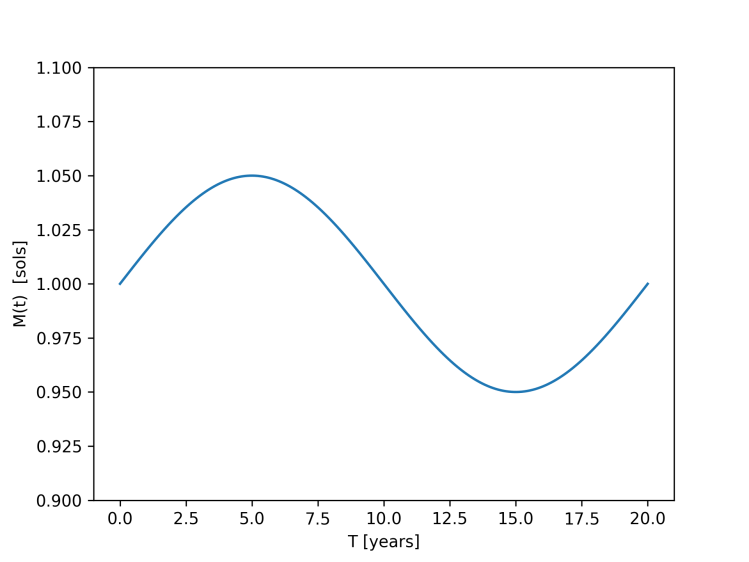
Let’s consider the behavior of orbits around a star whose mass changes over time. Let’s assume the mass of the star changes over time periodically with some timescale and some amplitude . It’s worth saying at the offset that this situation is highly unphysical. While it’s certainly the case that stars can lose mass over time (as happens during the RGB and AGB phases of stellar evolution) or gain mass (as may happen during stellar formation). These processes tend to be monotonic – either decreasing or increasing the mass of the star in a consistent way. It’s extremely difficult to propose a physical process that results in the mass of the star oscillating in the way we model. Therefore this effect is more of a mathematical curiosity than relevant to a real physical system. That said, the relative simplicity of the system lets it serve as a nice example of resonant phenomena more broadly.

To see the effects of this oscillation on orbiting planets we integrate for 1000 oscillation periods a series of planets on initially circular orbits around the star. We treat each particle as massless so it does not influence its neighbors. We choose the oscillation period of the star to be 20 years, and its amplitude to be 5%.

The results of the first few orbits of integration are shown in the animation below:

4

In the first few orbits of the integration, two effects can be seen. First is an overall oscillation in the size of all the orbits this is due to the short-term variation in the stellar mass over a given period. The second effect is a longer-term increase in the eccentricities of certain particles (those in light blue with semi-major axes near 2) are most noticeable here.

In animations of the full-term integrations which can be found (here as a gif and here as a video, download to avoid Google’s poor compression), we can see similar increases in the eccentricity of orange points. We can filter out the most dramatic examples by showing the period over time of only the most eccentric bodies (those whose eccentricity exceeds 0.5).

Here we see that the most eccentric bodies have two distinct orbital periods. One near 20 (the same timescale as the period of the star’s mass oscillation) and another near 40 (exactly double that period). This sort of behavior – excitation at integer multiples of a given frequency is characteristic of resonant phenomena.

We can explore this further by looking at how the eccentricities of all particles change as a function of their initial periods over the entire simulation. We can see large increases in eccentricity both at the 20-year and 40-year period and at an additional 10-year period.

While not a very physical example, the system is an excellent example of resonance

Github Link to Code: https://github.com/r-zachary-murray/archive/tree/master/Mass_Pumping