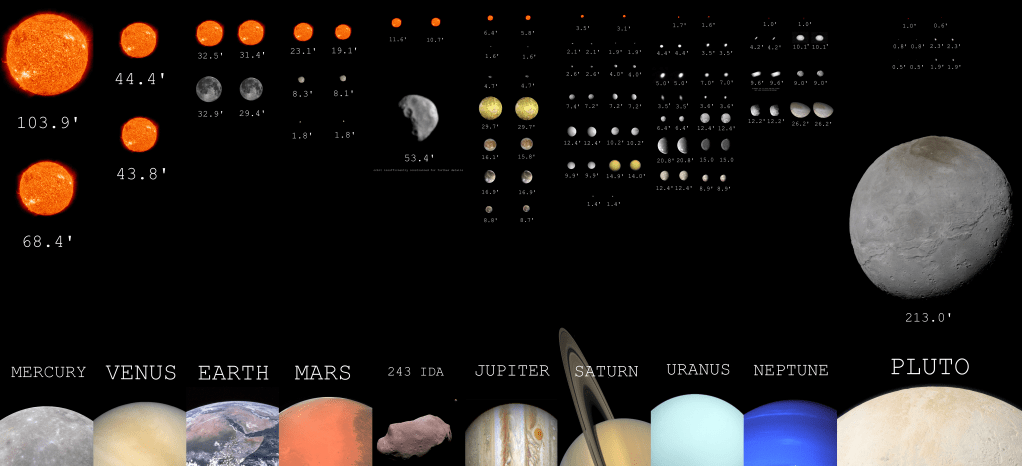
Angular Size of Moons from their Primaries

The angular diameters of nearby solar system objects to the planets, Pluto and the asteroid 243 Ida. All the bodies have the same relative scale, but the primaries do not. Click here for full size.

This graphic shows the relative angular diameters of the sun and natural satellites from different bodies in the solar system. Most bodies are shown twice to show their maximum and minimum angular extents, the exceptions are Dactyl (since it’s orbit is not well constrained), and Charon (since it’s orbital eccentricity is too low to cause much of a change). The elongation of the moons of Neptune is due to the long exposure times needed to capture them, they are scaled assuming the elongated shape is diameter of the moon – in reality these objects would be somewhat differently shaped once motion blur is accounted for – but their sizes are correct as shown. All the angular diameters are to scale relative to each other, but the primaries themselves are not to scale. A few interesting things about the above diagram is to see that total solar eclipses are impossible on only 3 of the chosen bodies, Mercury & Venus – due to neither planet having a moon, and Mars – since it’s moons are too small. An observer on every other body could in principle view a total solar eclipse by one moon or the other. (Surprisingly this includes 243 IDA!)

Interestingly, all of the Galilean moons are large enough to cause total solar eclipses, with the next largest moons being slightly too small. The major moons of Saturn can do the same, and by the time one is as far from the sun as Uranus and Neptune minor moons start becoming sufficiently large relative to the sun to cause total eclipses. On Pluto the situation is even more extreme with tiny moons like Nix (50 km across) and Hydra (51 km across) both capable of causing total eclipses. (This doesn’t necessarily mean the necessary alignment is likely – or even possible, but they have the diameter to do so in principle.)

Luckily we can check some of these calculations against real data – at least for Mars.

Eclipses involving Mars’ moons Phobos and Deimos as seen by the Curiosity rover. Here’s the NASA release

It looks like the relative scale of the Sun, Phobos and Deimos match rather well with the predictions in the graphic!