An odd little Fourier series

Consider the following Fourier series, $\sum_{k=1}^{n} \frac{sin(2 \pi k x)^n}{k}$ . This series has a peculiar property in that its even and odd sums converge to very different functions.

Let’s explore this further by comparing this sum to more pedestrian examples. Consider $\sum_{k=1}^{n} \frac{x}{2^k}$ , as long as $x < 1$ converges to $x$ as $n -> \infty$ . We can split this sum up into even and odd partial sums. That is – we choose to plot the function only when n is even or odd.

Unsurprisingly, wether we take even or odd partial sums, the total converges to the same value of $x$ .

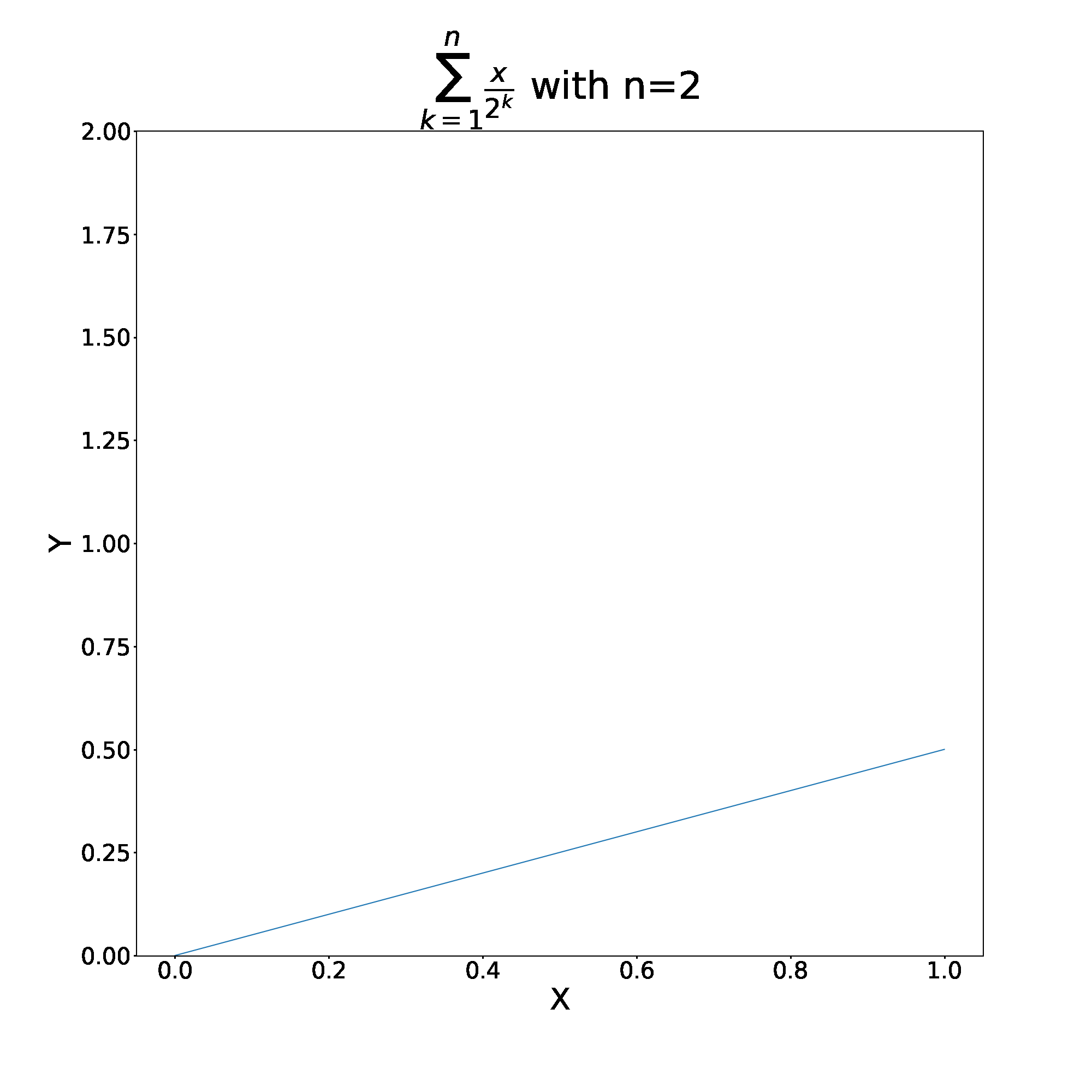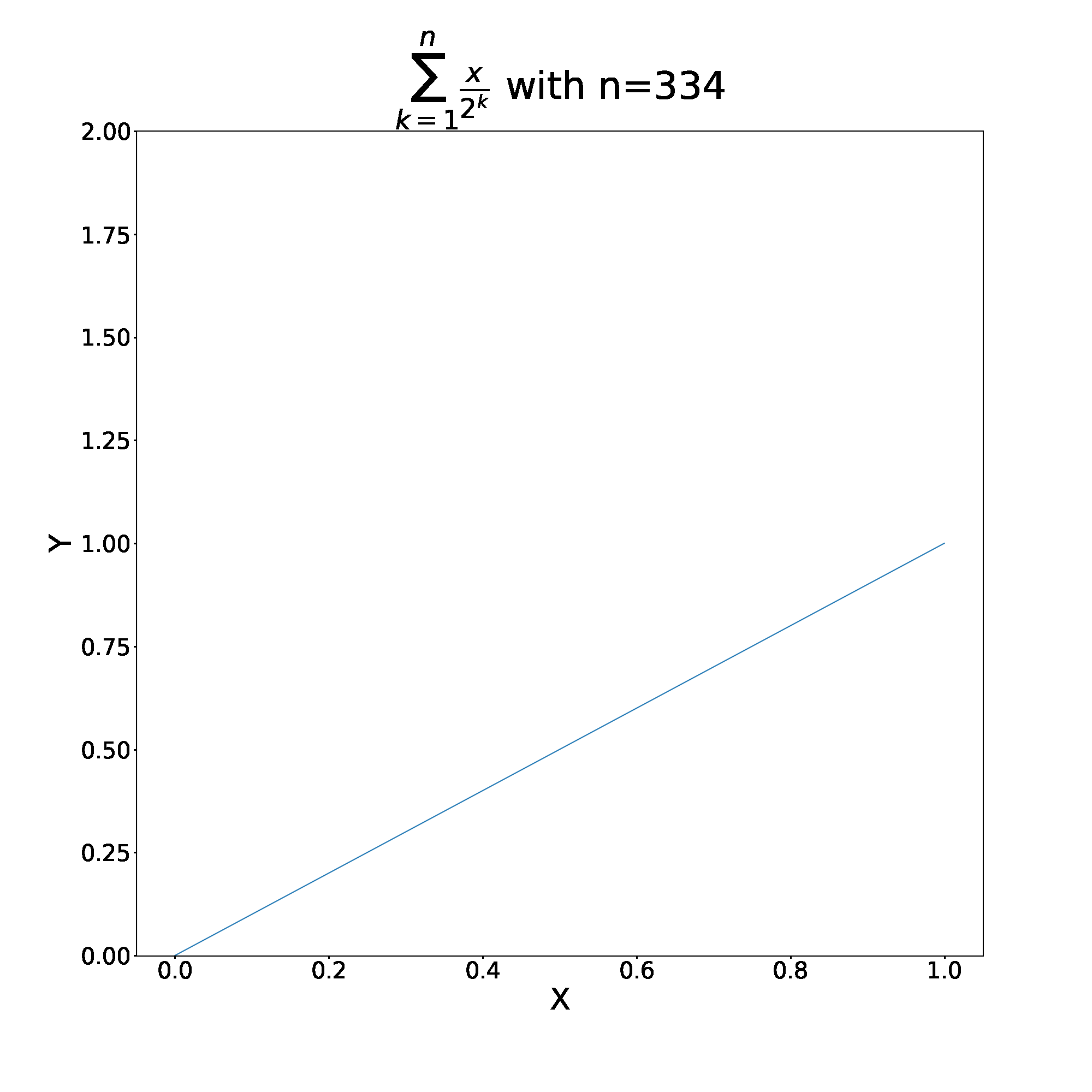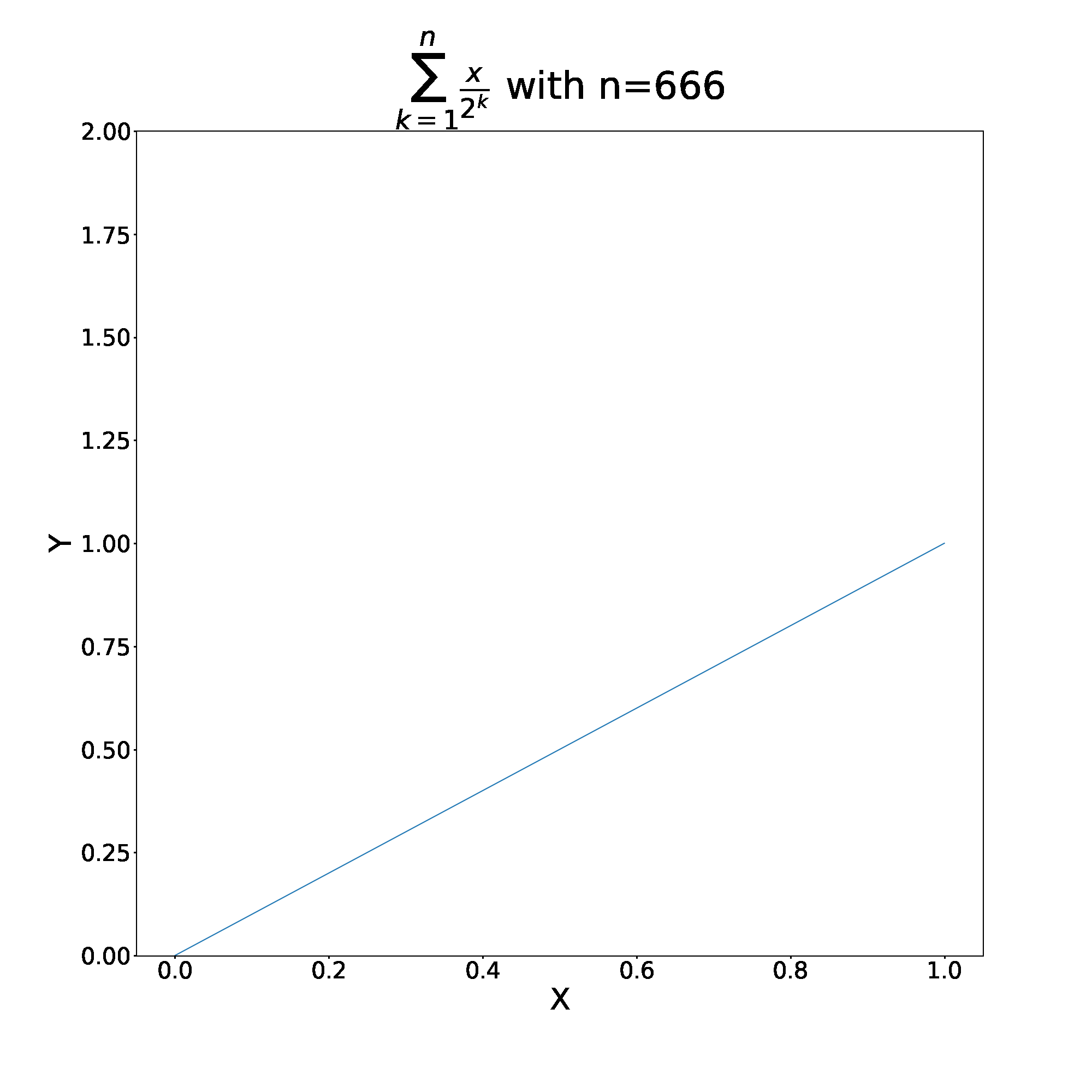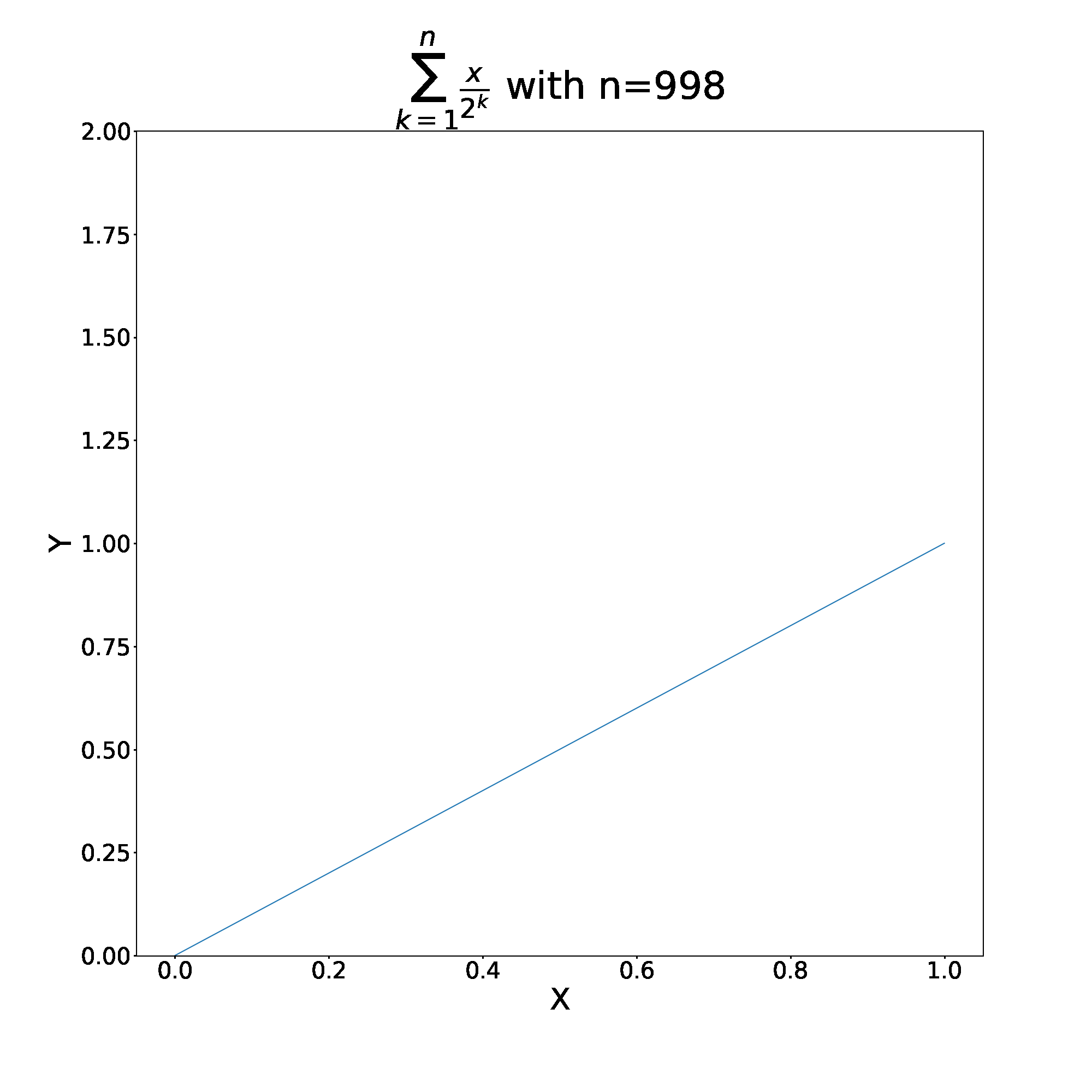
However, if we consider the behavior of the fourier series in question, $\sum_{k=1}^{n} \frac{sin(2 \pi k x)^n}{k}$ , we get very different behavior.

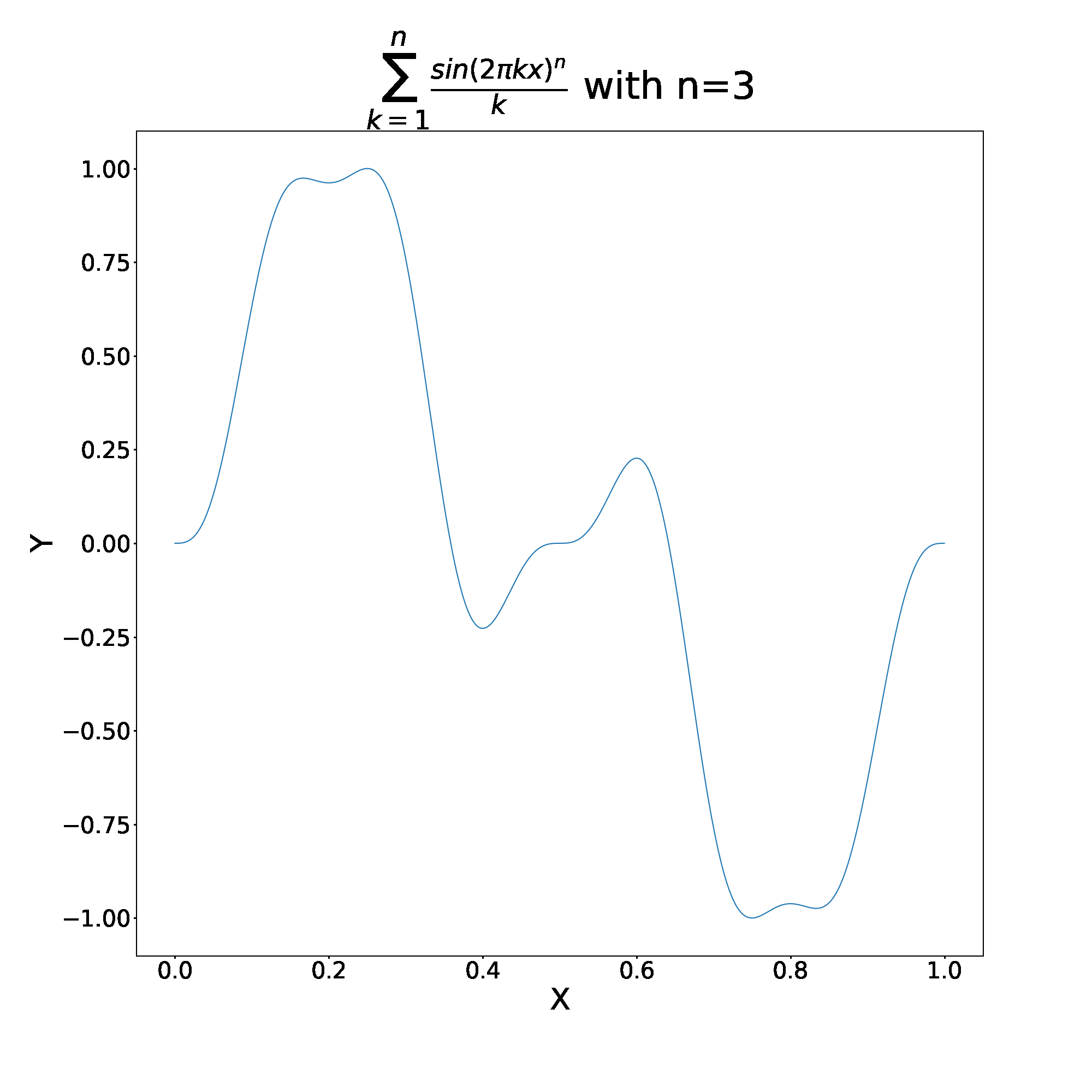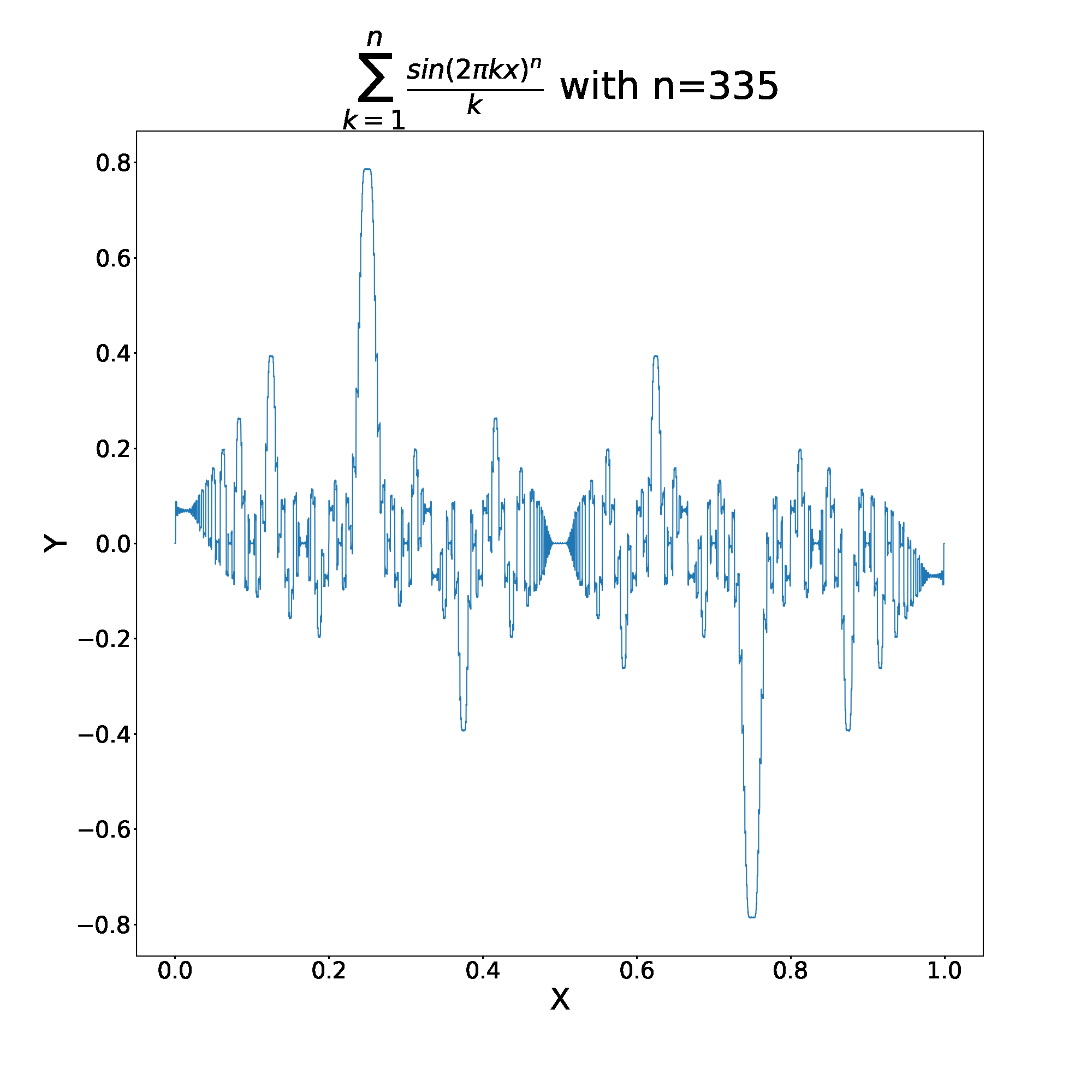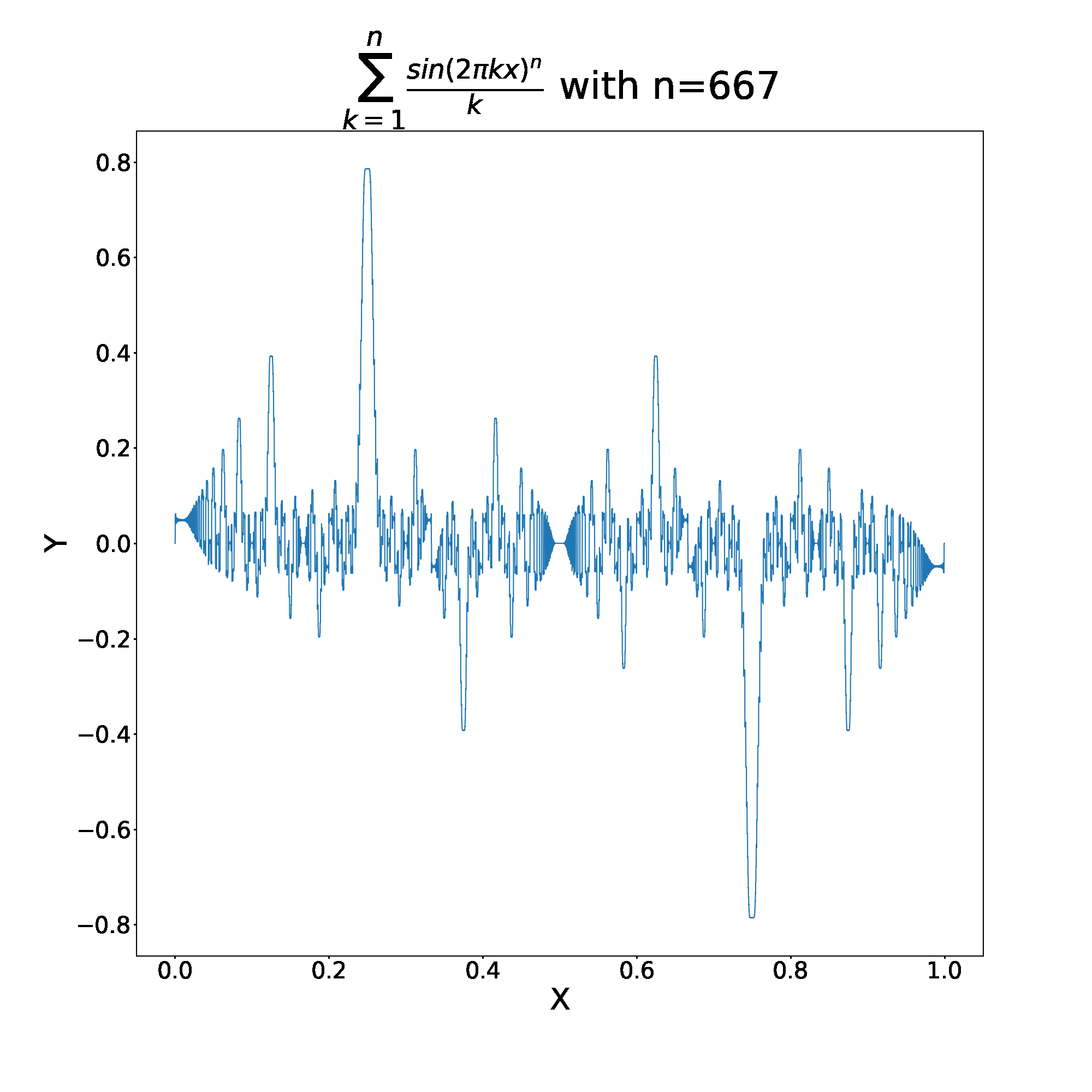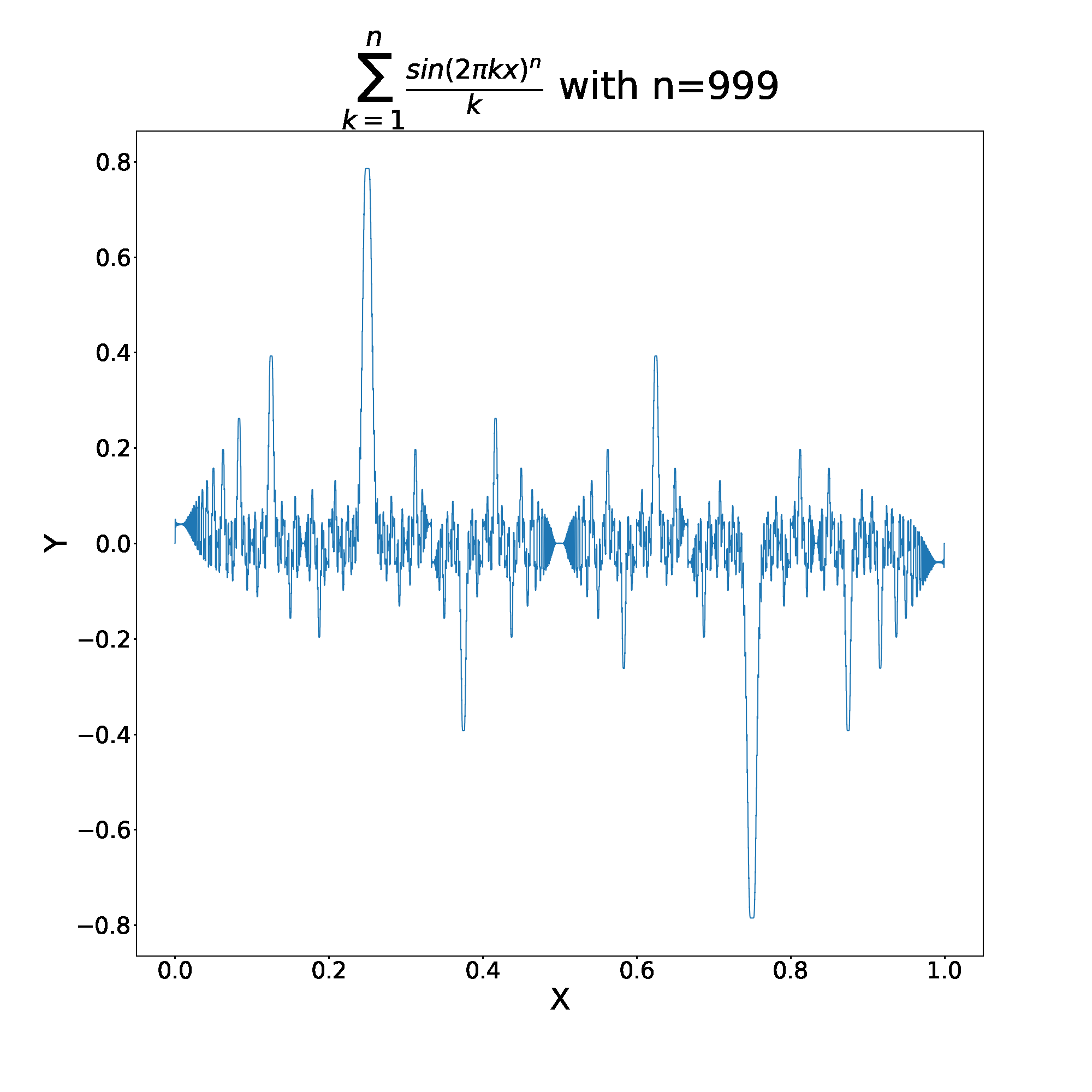
This function behaves very differently, the even and odd partial sums still converge, but in this case, converge to totally different functions. How interesting!

Github Link to Code: https://github.com/r-zachary-murray/archive/tree/master/sinusoid_convergence_animation