A Strange Integral

A Strange Integral

I recently came across the following integral $\int_0^\infty \frac{sin(x!)}{x!} dx$ . Here the factorial is understood to be extended to the entire real domain via the gamma function $x! = \Gamma(x+1)$ , with $\Gamma(x) = \int_0^\infty t^{x-1} e^{-x} dx$ .

There’s no obvious way to integrate this analytically, but it can be integrated numerically and the result is about 1.61. That’s a familiar number! This result is very nearly the golden ratio, $\phi = \frac{1+\sqrt{5}}{2}$ ! This raises the question – could it be that this integral converges exactly to $\phi$ ? Without an analytic form, we’re forced to use numerical methods and unfortunately, this integral is extremely poorly behaved and is highly oscillatory.

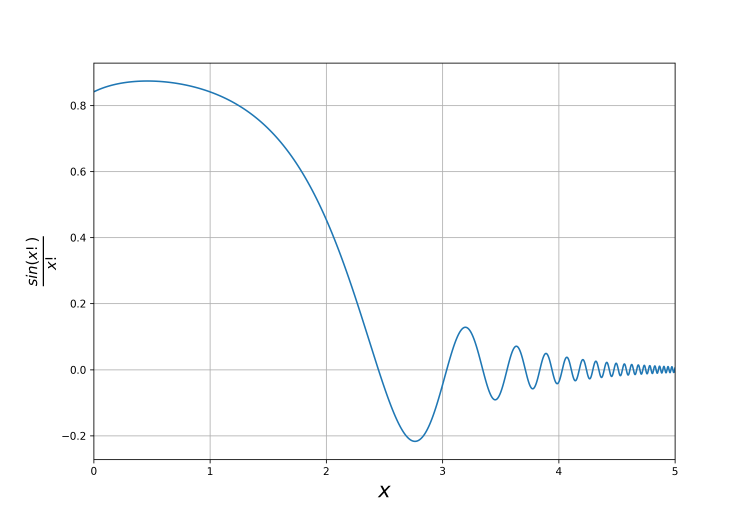
The behavior of the integrand for 0 < x < 5. It damps quickly and is extremely tough to integrate numerically.

The most naive way of integrating such a function would be with a Riemann sum. However, in this case, the highly oscillatory nature of the integral would seriously impede the convergence of such a simple method. A better alternative is to use the quad integrator in scipy’s integrate library. This integrator works using an adaptive quadrature method and hopefully will accurately fit all the little bumps in the function. Since we can’t integrate fully out to infinity, we’ll instead integrate up to some $z$ so our integral becomes $\int_0^z \frac{sin(x!)}{x!} dx$ and hope for convergence. The results of this experiment are shown below.

The new approximate integral versus the golden ratio (left panel) and the difference between them (right panel)

While the integral certainly converges – and we now have enough precision to tell it isn’t equal to the golden ratio – there’s still quite a bit of ‘noise’ for large $z$ . Looks like even the adaptive method is struggling a bit on this function. However, we can approximate the true value of the integral, by taking the median value of the results over some range. If we choose the range 20 < $z$ < 40 (large enough to converge, but not large enough to encounter some of the larger errors) that value is 1.6122, very close to the golden ratio of 1.6180 – with a difference of only about 0.5%. That’s surprisingly close!

Github Link to Code: https://github.com/r-zachary-murray/archive/tree/master/Odd_Integral